In the picture you can see two same triangles have 4 parts just arranged differently.
So, how does the square hole in second triangle forms. Amazing isn't it. Think for a while and see the solution below.
The key to the puzzle is the fact that neither of the 13×5 "triangles" is truly a triangle, because what appears to be the hypotenuse is bent. In other words, the "hypotenuse" does not maintain a consistent slope, even though it may appear that way to the human eye. A true 13×5 triangle cannot be created from the given component parts.
The four figures (the yellow, red, blue and green shapes) total 32 units of area. The apparent triangles formed from the figures are 13 units wide and 5 units tall, so it appears that the area should be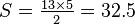 
units. However, the blue triangle has a ratio of 5:2 (=2.5:1), while the red triangle has the ratio 8:3 (≈2.667:1), so the apparent combined hypotenuse in each figure is actually bent. So with the bent hypotenuse, the first figure actually occupies a combined 32 units, while the second figure occupies 33, including the "missing" square.
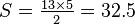units. However, the blue triangle has a ratio of 5:2 (=2.5:1), while the red triangle has the ratio 8:3 (≈2.667:1), so the apparent combined hypotenuse in each figure is actually bent. So with the bent hypotenuse, the first figure actually occupies a combined 32 units, while the second figure occupies 33, including the "missing" square.
The amount of bending is approximately 1/28th of a unit (1.245364267°), which is difficult to see on the diagram of this puzzle. Note the grid point where the red and blue triangles in the lower image meet (5 squares to the right and two units up from the lower left corner of the combined figure), and compare it to the same point on the other figure; the edge is slightly under the mark in the upper image, but goes through it in the lower. Overlaying the hypotenuses from both figures results in a very thin parallelogram with an area of exactly one grid square -- the same area "missing" from the second figure.
